Límites laterales

Límites por la izquierda, por la derecha y límite de la función

Para determinar el valor del límite del ejemplo de la lección anterior de "Aproximaciones sucesivas" hemos seguido en realidad un doble camino:

• Nos hemos acercado a x=3 por la izquierda, es decir, tomando valores ligeramente menores que 3, y...nos hemos acercado también por la derecha, es decir, tomando valores ligeramente superiores a 3

Como ambos procesos nos llevaban al mismo valor de la función, concluíamos que limx→3x2−4x+32x−6=1. Lo que hemos hecho, en realidad, es calcular los límites laterales:

El valor del límite de una función f(x) cuando x tiende a a por la izquierda es el valor al que se acerca y=f(x) cuando x se acerca a a tomando valores menores que a. Se denota:

limx→a−f(x)=L

Observa algunos ejemplos:

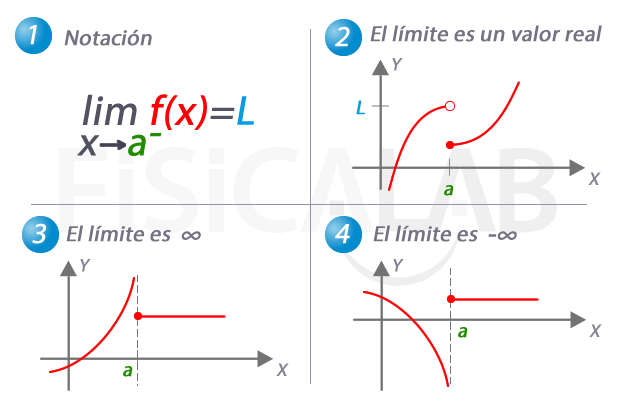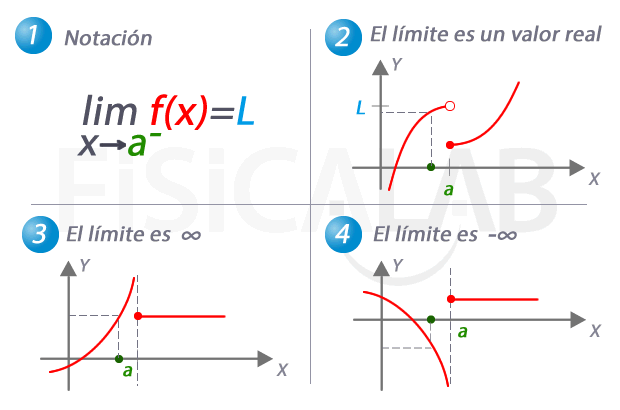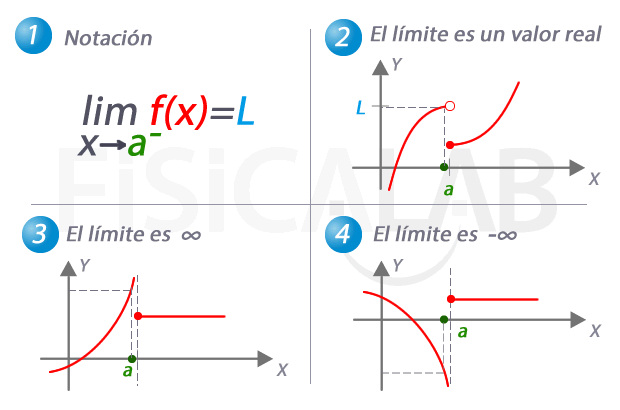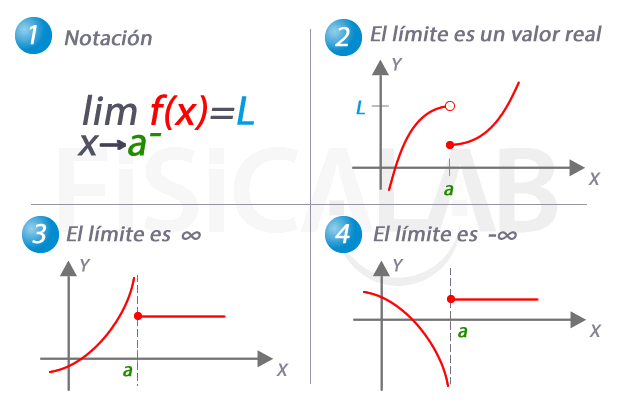
Límite lateral por la izquierda de una función

En 1, la notación utilizada para referirnos al límite de una función cuando x se aproxima a a por la izquierda. En 2, 3 y 4 tenemos tres ejemplos distintos. En 2 el límite es una valor real concreto, L. Observa como, de nuevo, el valor del límite no coincide con el de la función en el punto. En 3, a medida que nos aproximamos a a por la izquierda, los correspondientes valores de y son cada vez mayores. Es el caso en el que el valor del límite lateral es infinito. En 4, el caso complementario, con un límite lateral de menos infinito.

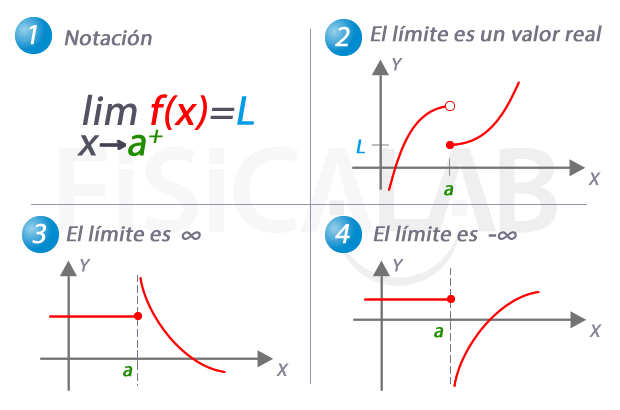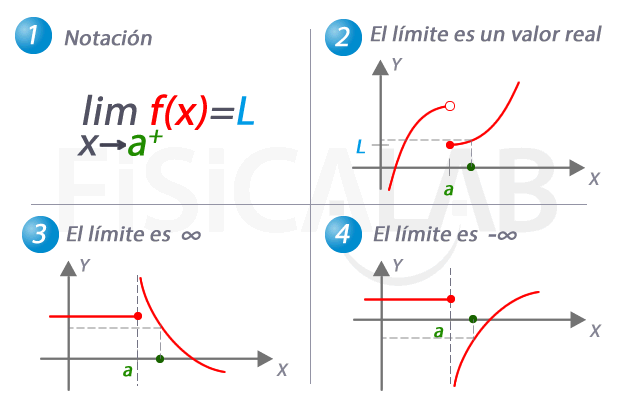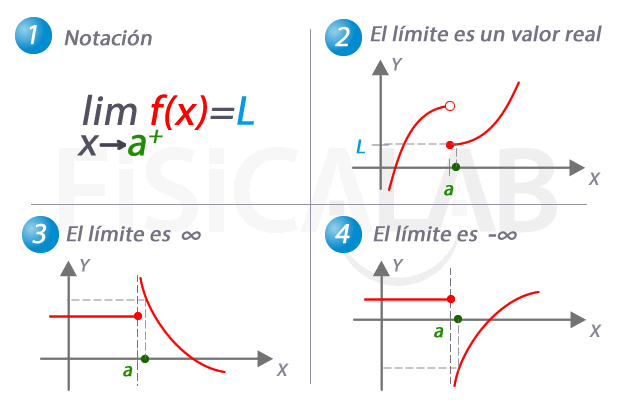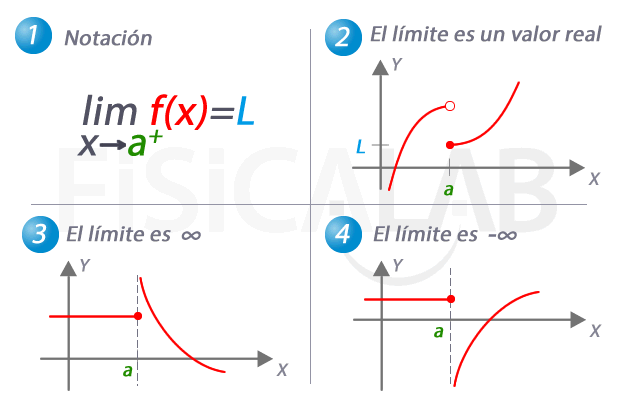
El valor del límite de una función f(x) cuando x tiende a a por la derecha es el valor al que se acerca y=f(x) cuando x se acerca a a tomando valores mayores que a. Se denota:

limx→a+f(x)=L

Donde:

• f(x) : es la función cuyo límite por la derecha estoy calculando
• x→a+: se lee "x tiende a a por la derecha", es decir, con valores mayores que a. Ten presente que, por ejemplo, 1.001 está a la derecha de 1, pero -0.99 está a la derecha de -1
• L : Es el valor del límite lateral. Puede ser un número real cualquiera, pero también infinito ∞ o menos infinito -∞

Observa algunos ejemplos:

Límite lateral por la derecha de una función

En 1, la notación utilizada para referirnos al límite de una función cuando x se aproxima a a por la derecha. En 2, 3 y 4 tenemos tres ejemplos distintos. En 2 el límite es una valor real concreto, L. Observa como, de nuevo, el valor del límite coincide en este caso con el de la función en el punto. En 3, a medida que nos aproximamos a a por la derecha, los correspondientes valores de y son cada vez mayores. Es el caso en el que el valor del límite lateral es infinito. En 4, el caso complementario, con un límite lateral de menos infinito.

Actividad evalúa tu conocimiento (50 ptos):

Evalúa tu conocimiento contestando el siguiente formulario:

Actividad de repaso (50 ptos):

Observa la siguiente imagen, ¿cuál es el limite por la derecha y por la izquierda de la función cuando x tiende a 0?

De acuerdo a lo visto en clase sobre límites laterales, ¿Por que se obtienen esos resultados?.

Comenta en la parte de abajo tu respuesta y compara con la de tus compañeros.