Conjunto complemento
Conjunto complemento
En un conjunto Universo de referencia un conjunto complementario (o complemento de un conjunto) es otro conjunto que contiene todos los elementos que no están en el conjunto original definido.
Entonces, para poder determinar los elementos de un conjunto complementario, es necesario especificar el Conjunto Universo de referencia.
Veamos un ejemplo:
Si el conjunto universo es
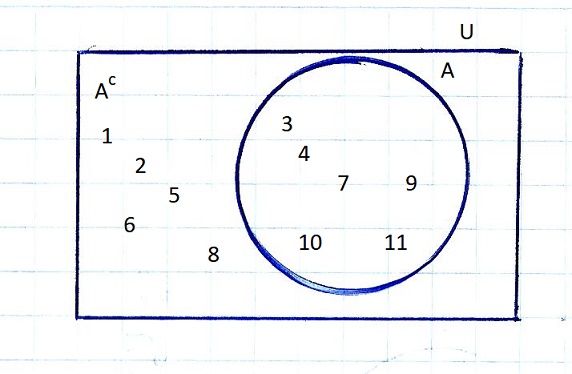
U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 }
y tenemos dentro el subconjunto
A = { 3, 4, 7, 9, 10, 11 },
entonces el Complementario de A (que se escribe como Ac) respecto del conjunto universo ( U ), está formado por los elementos de este universal que no están en A.
¿Cuáles elementos de U no están en A?
Ac = { 1, 2, 5, 6, 8 }
Los conjuntos A ={ 3, 4, 7, 9, 10, 11 } y Ac ={ 1, 2, 5, 6, 8 } son complementarios.
Reproduce el siguiente video:
-->Conjunto complemento (Da clic aquí)
Ejercicios de repaso (50 puntos):
a) tomamos como conjunto universo a Z (números enteros) entonces quedaría
ResponderBorrarU= (-infinito a infinito)
A= (numero entero positivo, por ejemplo 10)
A´=(- infinito excepto el 10 hasta infinito)
b) primeramente desarrolle los conjuntos para encontrar cuales eran sus elementos
U= (1,2,3,4,5,6,7,8,9.........,40)
A=(6,7,8,9,10,11,12,13,14,15,16,17,18)
A´=(1,2,3,4,5,19,20,21,22,23........,40)
c) Desarrolle los conjuntos para ver cuales eran sus elementos
U=(1,2,3,4,5,6,7.....,30)
A=(numero entero positivo por ejemplo 5)
A´=(1,2,3,4,6,7,8,9,10,11,..........,30)
DIEGO ARMANDO LOPEZ MARTINEZ
BorrarAldo Jesus Vazquez Campos CLAVE UNICA: 340146
ResponderBorrarResolucion del ejercicio:
A) me dice que x es un numero positivo entero esto abarca a todos los numeros positivos empezando desde el 1 R={ 1, 2, 3 al infinito}
B) obtengo el conjunto del universo U que me marca que son los numeros que sean mayor he igual que 1 y menor he igual que 40.
U={1,2,3,4,5,6,7,8,9,10..........asta....40}
conjunto del universo de A= mayor he igual que 6, menor he igual que 18.
A= {6,7,8,9,10,11,12,13,14,15,16,17,18}
Conjunto de A= Seria aquellos numero que no se repiten entre el conjunto del universo U y A y se localiza con la formula
R= A´= U - A A´={1, 2, 3, 4, 5, 19, 20.... corrido a 40} los numero que no tomaria son los que me da en el conjunto A de 6 a 18.
C) Obtengo el conjunto del universo
U = {1,2,3,4,5,6,7,8......... continuo asta 30}
A= Todos los numero positivo par, me da a entender que tomaria todo aquellos numeros pares que se encuentran entre 1 al 30
A= {2,4,6,8,10,12,14,16,18,20,22,24,26,28,30}
A´= {1,3,5,7,9,11,13,15,17,19,21,23,25,27,29}
a) En el inciso a tenemos que tomar en cuenta solo los números enteros positivos y no negativos.
ResponderBorrarPor lo que esto tendería a tener como respuesta:
Todos los números enteros positivos mayores que 1, hasta el infinito.
b) Es simple, solamente había que desarrollar el conjunto, como el universo va desde 1 hasta el 40.
Y el conjunto A va desde (6....18).
Solamente sacamos las unidades que no aparecen.
Quedando:
A': (1,2,3,4,5,19......40).
c) Se realiza como el anterior, como el universo sin todos los números del 1 hasta el 30. Y el conjunto A son los números pares desde el 1 hasta el 30.
Por lo tanto como conclusión, tendremos que A' el resultado serían todos los números impares que van desde el 1 hasta el 30.
A'= (1,3,5,7,9,11,13,15,17,19,21,23,25,27,29)
Carlos Iván Méndez López
CLAVE: 348012
Angel Felipe Santiago Rodriguez CLAVE:346493
ResponderBorrarActividad 1: Respuesta: A {2.4}
Se le dio al conjunto de U {1,2,3,4,5} lo cual su complemento seria {2,4}
Actividad 2: Respuesta A:{0,2,6,13}
Se saco su numero por extensión de ambos conjuntos lo cual determina el numero de conjuntos de A1.
Actividad 3: Respuesta A1: {0,2,15}
Se saco primero el numero por extensión de U y el numero de A seria 2 por que equivale a un numero par. y de esa manera se encontraría el valor de A1
Su numero para dividir la extension de la actividad 2 fue por 3 y el de la actividad 3 fue por 2
BorrarJESÚS RANGEL CAMACHO
ResponderBorrarA)¿Cuál es el complemento de A?
El A nos indica que son todos los números positivos enteros y por ende coloque estos
A={1,2,3,4,5,6,7,8,9,10,...}
B)¿Cuál es el conjunto de A¹?
Escribí todos los números entre el 6 al 18 ya que este sería nuestro conjunto donde A={6,7,8,9,10,11,12,13,14,15,16,17,18}
C)Hallar A'
Aquí nos expresa que A' son los números impares positivos, por ende serían A'={2,4,6,8,10,12,14,16,18,20,22,24,26,28,30}
Clave única:342351
Carlos Avalos Jerónimo
ResponderBorrarA) me dice que x es un numero positivo entero que empieza por el 1 R={ 1, 2, 3 al infinito}
B) desarrolle el conjunto U que son los números que sean mayor e igual que 1 y menor e igual que 40.
U={1,2,3,4,5,6,7,8,9,10..........hasta....40}
A= mayor e igual que 6, menor e igual que 18.
A= {6,7,8,9,10,11,12,13,14,15,16,17,18}
A= Seria los números que no se repiten entre el conjunto U y A={1, 2, 3, 4, 5, 19, 20.... 40} .
C) desarrolle los conjuntos
U = {1,2,3,4,5,6,7,8.....30}
A= Todos los numero positivo impar del 1 al 30 {1,3,5,7,9,11,13,15,17,19,21,23,25,27,29}
En el inciso A el complemento de A es
ResponderBorrarA son todos los números positivos de (1 hasta +infinito)
En el inciso b
Sacamos los números de U que van desde 1 hasta 40
Y los números de A que van desde 6 a 18
Después sacamos los números de U que no estaban en A
Respuesta = todos los números naturales de (1,5) y de (19,40)
Inciso C
Sacamos los números de U
Que van de (1 ,30)
Y marca que en A son números positivos pares
Los números de U que no pertenece a A son números impares del (1,29)
Entonces Aprima es igual a números naturales impares de (1,29)
Jorge David Izaguirre Cruz
ResponderBorrarClave única 345467
En el a) el complemento es (1, al infinito) pues son puros positivos
En b) el conjunto de A se separan los numeros de u= (1,2,3,4,5,6,......40) y A=(6,7,8,9,10,11,12.......18)
El conjunto seria (1,2,3,4,5,19,20,21,22,23,25..........,40)
C) {1,3,5,7,9,11,13,15,17,19,21,23,25,27,29}
Se saco primero el numero por extensión de U y el numero de A serian los numeros pares y de esa manera se encontraría el valor de A1
a) A es igual a un numero entero positivo pero como no especifica cual quieres decir que U={1,2,3,4,5,6...}
ResponderBorrarb) Yo simplifique los conjuntos, U=(1,2,3,4,5...40} y A={6,7,8,9,10...18}, A' es igual a todos los números del 1 al 40, excepto del 1 al 18, así queda el conjunto A'= {1,2,3,4,5,19,20,21,22...40}. Así A y A' son complementarios.
c)U={1,2,3,4,5...30} y A={2,4,6,8,10..30}, con esto se encuentra A'={1,3,5,7,9...29}. De esta manera A y A' son complementarios.
Adrián Feliciano Crescencio
ResponderBorrarA)X es un numero positivo entero esto abarca a todos los numeros positivos empezando desde el 1 R={ 1, 2, 3 al infinito}
B)A:{0,2,6,13}
Se saco su numero por extensión de ambos conjuntos lo cual determina el numero de conjuntos de A1
C)U={1,2,3,4,5...30} y A={2,4,6,8,10..30}, con esto se encuentra A'={1,3,5,7,9...29}. y A y A son complementarios
A) Para responder el primero dice que x es un numero positivo y no marca hasta donde acaba solo que son numeros positivos entonces quedaria A=(1,2,3,4........) ya que los numeros positivos son infinitos
ResponderBorrarB) primero obtengo el conjunto universo num. posotivos U=(1,2,3,4.......40)
despues dice que mayor igual que 6 menor igual que 18 A=(6,7,8,9.....18)
R=(1,2,3,4,5,19,20,21......40)
Aqui no se toma en cuenta el conjunto ya que los elementos delsegundo conjunto no pertenecen al primer conjunto
C)primero se obtienen los conjuntos
U=(1,2,3,4,5.........30)
A=(0,2,4,6,8,10,12,14.......30)
R=(1,3,5,7,9,11,13,15,17,19,21,23,25,27,29)
MIGUEL ÁNGEL ERASTO ANTONIO
ResponderBorrarCLAVE: 347576
A) , Tomamos como conjunto universo a Z (números enteros) , entonces quedaria
U= (INFINITO A INFINITO)
A= (NUMERO ENTERO POSITIVO 10)
A¹= (- INFINITO EXCEPTO EL 10 HASTA INFINITO)
B) es Simple solamente habia que desarrollar el conjunto el.conjunto como el.univerdo va desde (6....18)
Solo sacamos las unidades que no aparecen quedando
A¹: (1,2,3 ,4 ,5,19......40)
C) A1: {0,2,15}
Se saco primero por el numero de extensión de U y el numero de A serian 2 por que equivale a un numero par y de esa manera se encontraría el valor de A1
Rocío Lizeth Hernández Flores
ResponderBorrarClave: 341396
a) me dice que A son todos los números pares enteros hasta el infinito, entonces su conjunto sería todos los números negativos y todos los números impares enteros hasta el infinito
Ac={ ...-2,-1,0,1,3,5,7,9,11...}
b)Desarrollando el conjunto quedaría Ac={1,2,3,4,5,19,20,21,22,23,24,25...40}
c)La indicación dice que a=es un número par positivo. entonces sería
A={2,4,6,8,10...}
U={1,2,3,4,5,6,7,89...30}
Lo que haría que Ac={1,3,5,7,9,11,13,15,17,19,21,23,25,27,29}
a) tome como conjunto universo a Z (números enteros) entonces quedaría
ResponderBorrarU= (-infinito a infinito)
A= (numero entero positivo)
A´=(- infinito excepto el 10 hasta infinito)
b) desarrolle los conjuntos para encontrar cuales eran sus elementos
U= (1,2,3,4,5,6,7,8,9,10...,40)
A=(6,7,8,9,10,11,12,13,14,15,16,17,18)
A´=(1,2,3,4,5,19,20,21,22,23...,40)
c) Después desarrolle los conjuntos para ver cuales eran sus elementos
U=(1,2,3,4,5,6,7,8,9,10..,30)
Ac=(1,3,5,7,9,11,13,15,17,19,21,23,25,27,29)