3.1.3 Técnicas para calcular limites: Límites por factorización
CASOS DE FACTORIZACIÓN
DIFERENCIA DE CUADRADOS
Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.
Se tiene el siguiente ejercicio:
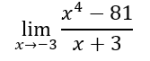
Para comprobar si es una indeterminación, reemplazamos -3 en x:
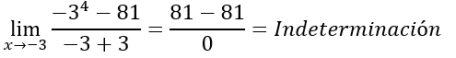
Como es una indeterminación, procedemos a verificar los casos de factorización que podemos usar, en este caso diferencia de cuadrados perfectos y simplificamos la función: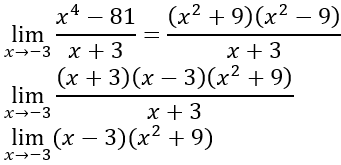
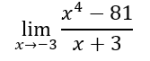
Para comprobar si es una indeterminación, reemplazamos -3 en x:
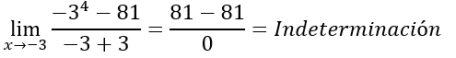
Como es una indeterminación, procedemos a verificar los casos de factorización que podemos usar, en este caso diferencia de cuadrados perfectos y simplificamos la función:
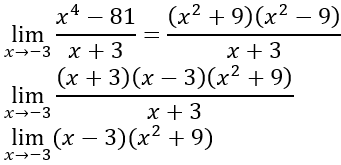
Una vez simplificada la función procedemos a reemplazar x, como el denominador ya fue simplificado, la indeterminación ha sido levantada.
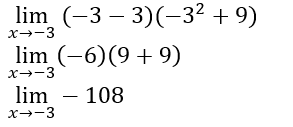
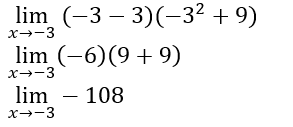

SUMA O DIFERENCIA DE CUBOS PERFECTOS
Para realizar la aplicación de límites en un caso donde se tenga una suma o diferencia de cubos perfectos es necesario realizar ciertas operaciones ya que, muchas veces, al reemplazar el límite, puede dar como resultado una indeterminación.
Se tiene el siguiente ejercicio: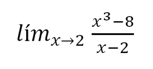 Para verificar si es una indeterminación se procede a reemplazar el valor del límite que es “2”:
Para verificar si es una indeterminación se procede a reemplazar el valor del límite que es “2”:
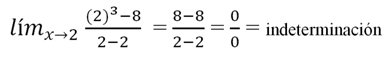 Como es una indeterminación se procede a descomponer en factores al numerador, siendo este una diferencia de cubos perfectos, para esto hay que saber que la forma de descomponer se da de la siguiente manera:
Como es una indeterminación se procede a descomponer en factores al numerador, siendo este una diferencia de cubos perfectos, para esto hay que saber que la forma de descomponer se da de la siguiente manera: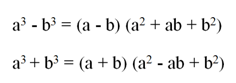
Se tiene el siguiente ejercicio:
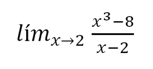 Para verificar si es una indeterminación se procede a reemplazar el valor del límite que es “2”:
Para verificar si es una indeterminación se procede a reemplazar el valor del límite que es “2”: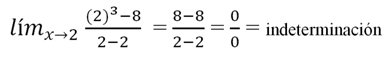 Como es una indeterminación se procede a descomponer en factores al numerador, siendo este una diferencia de cubos perfectos, para esto hay que saber que la forma de descomponer se da de la siguiente manera:
Como es una indeterminación se procede a descomponer en factores al numerador, siendo este una diferencia de cubos perfectos, para esto hay que saber que la forma de descomponer se da de la siguiente manera: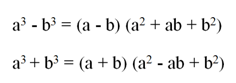
Sabiendo esto, lo siguiente a realizar es la descomposición del numerador.
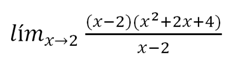 Ya habiendo descompuesto, finalmente se procede a simplificar los factores semejantes y a reemplazar el límite.
Ya habiendo descompuesto, finalmente se procede a simplificar los factores semejantes y a reemplazar el límite.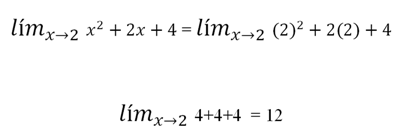
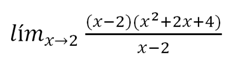 Ya habiendo descompuesto, finalmente se procede a simplificar los factores semejantes y a reemplazar el límite.
Ya habiendo descompuesto, finalmente se procede a simplificar los factores semejantes y a reemplazar el límite.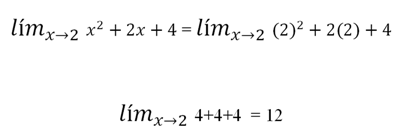

TRINOMIO DE LA FORMA (ax^2+bx+c)
La aplicación de la factorización en los limites se da cuando el resultado es de la forma 0/0 (indeterminación)
Cuando se sustituye el valor al cual tiende la variable en la función, es decir,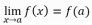 y el resultado es de la forma 0/0 es decir,
y el resultado es de la forma 0/0 es decir, 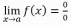 a este resultado se le llama indeterminación de la forma 0/0. Entonces para poder calcular el límite es necesario quitar esta indeterminación. Para quitar esta indeterminación lo que vamos a hacer es factorizar la función (en el caso en que se pueda) y después simplificar y obtener el límite.
a este resultado se le llama indeterminación de la forma 0/0. Entonces para poder calcular el límite es necesario quitar esta indeterminación. Para quitar esta indeterminación lo que vamos a hacer es factorizar la función (en el caso en que se pueda) y después simplificar y obtener el límite.
Cuando se sustituye el valor al cual tiende la variable en la función, es decir,
Cuando en el límite se presenta este caso de factorización se lo puede resolver de 2 maneras:
- Método de tanteo: (x+a) (x+b) =ax2+bx+c=0
- Formula general:
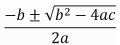
EJEMPLOS

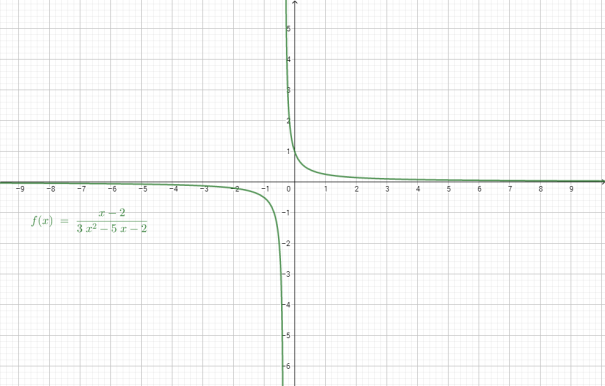

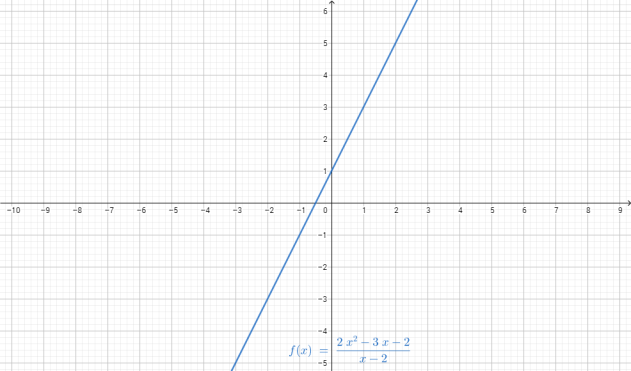
TRINOMIO CUADRADO PERFECTO
Un trinomio cuadrado perfecto, por brevedad TCP, es un polinomio de tres términos (también llamado trinomio) que resulta de elevar al cuadrado un binomio.
Todo trinomio de la forma:
Todo trinomio de la forma:
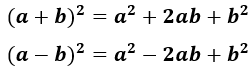
Siendo la regla: Cualquier suma de binomios al cuadrado es igual al cuadrado del primer término, más el doble del primer por el segundo término, más el cuadrado del segundo término. De lo anterior resulta que un trinomio será cuadrado perfecto siempre que se cumplan las siguientes condiciones:
El polinomio pueda ser ordenado en potencias descendentes de una variable.
Dos de los términos son cuadrados perfectos.
El otro término es el doble producto de las raíces cuadradas de los demás.
El primer y tercer término deben de tener el mismo signo
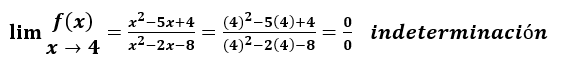
Levantar la indeterminación:
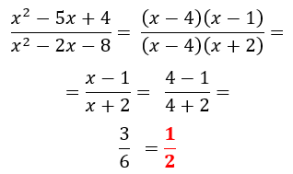
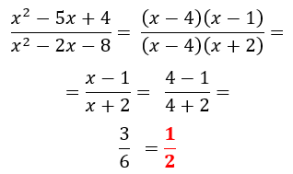
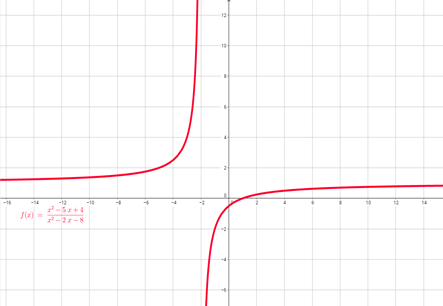
FACTOR COMÚN
Un polinomio tiene factor común cuando una misma cantidad, ya sea número o letra, se encuentra en todos los términos del polinomio.
Para efectuar el factor común hay que tomar en cuenta que con la parte literal “letras” se toma la que tenga el menor exponente de todas y en la parte numérica se saca el Máximo común Divisor.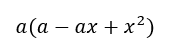
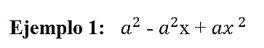
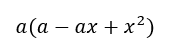 EJEMPLO CON LIMITES
EJEMPLO CON LIMITES
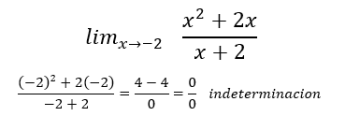 LEVANTAR LA INDETERMINACIÓN CON FACTORIZACIÓN
LEVANTAR LA INDETERMINACIÓN CON FACTORIZACIÓN
Para efectuar el factor común hay que tomar en cuenta que con la parte literal “letras” se toma la que tenga el menor exponente de todas y en la parte numérica se saca el Máximo común Divisor.
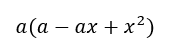
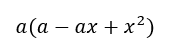 EJEMPLO CON LIMITES
EJEMPLO CON LIMITES 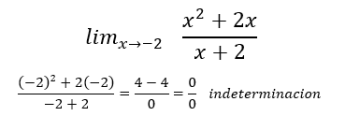 LEVANTAR LA INDETERMINACIÓN CON FACTORIZACIÓN
LEVANTAR LA INDETERMINACIÓN CON FACTORIZACIÓN 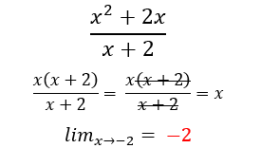
- Observa los siguientes vídeos:
Ejemplo 1
Ejemplo 2
Actividad evalúa tu conocimiento (50 ptos):
Contesta el siguiente formulario. (Da clic aquí)
Ejercicio de repaso (50 ptos):
Comenta tu resolución en la parte de abajo y compara con la de tus compañeros.


Salazar Castillo:
ResponderBorrar(x-1)(x-4)/(x+2)(x-4)= (x-1)/(x+2) = x tiende a 4 = (4-1)/(4+2) = 3/6 = 1/2 =0.5
Pérez Salazar-0278112
ResponderBorrarlim(x→4) ((x(x-1)-4(x-1))/(x(x+2)-4(x+2))
lim(x→4) ((x-1)-(x-4))/((x+2)-(x+4))
lim(x→4)=(4-1)/(4+2) = 3/6
lim(x→4)=1/2
Gonzalez Padilla 281757
ResponderBorrar((x-1)-(x-4))/((x+2)-(x+4))
(4-1)/(4+2):3/6
0.5
Simplificamos la ecuación x^2-5x+4/x^2-2x-8= x-1/x+2 sustituimos cuando x tiende a 4 = 4-1/4+2= 1/2
ResponderBorrarLópez flores soy este último comentario:3
Borrarlim x→4 = (x(x-1)-4(x-1)/(x(x+2)-4(x+2)
ResponderBorrarlim x→4 = (x-1)-(x-4)/((x+2)-(x+4)
lim x→4 =(4-1)/(4+2)
lim x→4= 3/6
lim(x→4)= 1/2= 0.5
SAMANTHA SANCHEZ MARTINEZ
ResponderBorrarPrimero al sustituir X nos damos cuenta que el resultado es 0/0 es indeteminada. Y facorizamos todo primero arriba y continuamos con abajo
Al factorizar queda al ultimo
(X-1)/(X+2)= 4-1/4+2= 3/6= 1/2
MEDINA RODRIGUEZ JUAN EDUARDO 234862 IER
ResponderBorrar((x-1)-(x-4))/((x+2)-(x+4))
(4-1)/(4+2):3/6
1/2
Nombre: Gonzalez Ortega Miguel Angel
ResponderBorrarClave: 234862
Carrera: IER
Limite Tiende x--->4
((x-1)-(x-4))/((x+2)-(x+4))
(4-1)/(4+2):3/6
1/2
cinthia contreras banda
ResponderBorrarprimero evaluamos el limite lo que nos da a cero, despues lo resolvemos de la siguiente manera
lim (x^2-x-4x+4x)/ x^2-2x-8)
lim (xx(x-1)-4x+4) / x^2+2x-4x-8)
lim (x-1)/(x+2)
lim (4-1)/(4+2)
= 1/2
Torres Castillo Israel--277491
ResponderBorrarlim(x→4) ((x(x-1)-4(x-1))/(x(x+2)-4(x+2))
((x-1)-(x-4))/((x+2)-(x+4))
=(4-1)/(4+2) = 3/6
lim(x→4)=1/2
Cristian Leija Sandoval - 283040 - IER
ResponderBorrar((x-1)-(x-4))/((x+2)-(x+4))
(4-1)/(4+2):3/6
0.5
Jesús Emmanuel Serrato Rodríguez
ResponderBorrar0311339 IER
lim(x→4) ((x(x-1)-4(x-1))/(x(x+2)-4(x+2))
lim(x→4) ((x-1)-(x-4))/((x+2)-(x+4))
lim(x→4)=(4-1)/(4+2) = 3/6
lim(x→4)=1/2
INGRID SHANTAL VAZQUEZ MARTÍNEZ_340559
ResponderBorrarlim(x-->4) ((x(x-1)-4(x-1))/(x+2)-4(x+2))
lim(x-->4)((x-1)-(x-4))/((x+2)-(x+4))
lim(x-->4)=(4-1)/(4+2)=3/6
lim(x-->4)=1/2
Yordy Hernández Velázquez
ResponderBorrarSolo se sustituye el valor de x por 4
X2-5x+4/X2-2x-8=
16-20+4/16-8-8=0/0
Osea la factorización es una indeterminacion por qué el resultado es 0/0
Manuel Alejandro Medellín Flores
ResponderBorrarVamos a sustituir el valor de x en la ecuación, en este caso x=4
Simplificamos
x^2-5x+4 / x^2-2x-8= x-1 / x+2
(4)-1 / (4)+2= 4/8= 1/2 o 0.5
Montserrat Alejandra Félix Mendoza
ResponderBorrarla función dice:
lim x-->4 x^2 - 5x + 4/ x^2 - 2x - 8
si solo sustituimos x en la ecuación el resultado sería
(4)^2 - 5 (4) + 4/ (4)^2 - 2 (4) - 8 = 20 - 20/ 16 - 16
= 0/0 lo que sería una indeterminación, por lo que es necesario factorizar quedando de la siguiente manera:
lim x-->4 x^2 - 5x + 4/ x^2 - 2x - 8
= (x - 4) (x - 1)/ (x - 4) (x - 2) = x - 1/ x + 2 = 4 - 1/ 4 + 2
= 3/ 6 o podemos simplificar dividiendo entre 3, lo que sería = 1/2
María Fernanda Martínez Hernández
ResponderBorrarlim(x-4) (x(x-1)-4(x-1)/(x(x+2)-4(x+2)
lim(x-4) (x-1)-(x-4)/(x+2)-(x+4)
Se elimina la indeterminación que es x-4
lim(x-4)=(4-1)/(4+2) = 3/6
lim(x-4)=1/2
LimiteX tiende a 4
ResponderBorrar(x-1)-(x-4)/(x+2)-(x+4)= (4-1)/(4+2)= 3/6= Simplificando es 1/2
Manuel Alejandro Medellín Flores
Sustituir el valor de x que es igual a 4:
ResponderBorrarX-1/X+2 = 4-1/4+2=1/2
Iliana betsahi Hervert Salazar.
Sustituimos el valor de x=4
ResponderBorrarX-1/x+2=4-1/4+2=1/2
Rosa Isela Álvarez Zuviri
Jonathan Sebastián Felipe para la resolución se sustituye por su valor buscado simplificarlo hasta optener el resultado
ResponderBorrarCesar uriel Hernández Rivera
ResponderBorrar1A clave: 347846
((X-1)-(x-4))- / ((x + 2)- (x + 4))
(4-1) / (4 + 2): 3.6
0.5